Oändlighetens smaragder förvirrar och fascinerar
Din bankkod, ditt personnummer, Shakespeares samlade verk … allt finns gömt i ett irrationellt tal.

Bild: Andreas Nilsson
Det oändliga har alltid fascinerat mänskligheten. Är universum till exempel oändligt stort eller är det begränsat? Och om det är begränsat, vad finns då bortom denna gräns?
Liknande frågor har man ställt sig inom matematiken. Det började med de naturliga talen, alltså 0,1,2,3,4 etcetera. Den här serien fortsätter in i evigheten, eftersom vilket tal man än väljer som det största alltid kan adderas med ytterligare tal, och vips har vi ett större tal. Med andra ord, det finns oändligt många heltal.
Matematiska skönheter
Detta är första delen av tre i artikelserien om matematiska skönheter. Läs den andra delen här.
Oändligheten har ett antal märkliga egenskaper. Fundera över vad som händer om vi skulle stryka alla jämna tal från denna lista? Ja då har vi kvar alla ojämna. Men det finns oändligt många både jämna och ojämna tal. Det innebär att om vi tar bort oändligt många tal (alla de jämna), från alla heltal har vi fortfarande oändligt många kvar, med andra ord:
Oändligheten minus oändligheten = oändligheten.
Oändlighetens vindlingar hyser fler smaragder. Låt mig påminna om operationen roten ur.
Roten ur 9 är alltså 3, eftersom om vi multiplicerar 3 med sig självt så får vi tillbaka nio. Det här gäller för alla tal. Roten ur 16 är sålunda 4, och roten ur 100 är 10.
Men fundera nu över vad som händer om man tar roten ur 2. Vilket tal multiplicerat med sig självt blir 2?
Här får man pröva sig fram. Testar man 1,4 hamnar man nära, eftersom 1,4 x 1,4 = 1,96. Vidare har vi att 1,5 x 1,5 = 2,25, så det blir något för stort. Roten ur 2 måste alltså vara större än 1,4 men mindre än 1,5. Letar man länge och väl, eller testar med miniräknare eller smartphone, kommer man fram till ett svar på ungefär 1,414213…
Antikens matematiker har intresserat sig för det här talet länge. Det har att göra med att det uppträder i geometrin på ett högst konkret sätt. Har man en kvadrat med sidorna ett blir diagonalen exakt lika med roten ur 2. Talet är sålunda också av stort praktiskt värde när man ska beräkna avstånd.
Redan babylonierna lyckades för 3 700 år sedan komma fram till en mycket bra approximation. Deras uppskattning skiljer sig från det korrekta värdet med ungefär en miljondel. Det är en imponerande prestation. En lertavla med detta resultat, kallad YBC7289, finns bevarad vid Yale Babylonian Collection.
Lite drygt tusen år senare verkade pythagoréerna, en grupp tänkare som hade samlats kring Pythagoras, i det antika Grekland. De ägnade sig åt matematik, filosofi, musik och andra sköna konster och de påminde också om ett slags sekt där de naturliga talen (heltalen plus nollan) utgjorde en form av ramverk, en byggställning kring vilken hela världen gick att byggas upp och förstå.
Tal som exempelvis 0,5 och 0,25 gick att skriva som kvoten mellan två heltal och på så sätt kunde man bygga upp aritmetiken. I pythagoréernas världsbild var alla tal antingen heltal eller kvoter mellan dem. I dag kallar vi dessa tal för rationella, det syftar på de tal som kan skrivas som en kvot mellan två heltal.
Men snart insåg pythagoréerna att talet roten ur 2 inte passade in i denna bild. Det kunde nämligen inte beskrivas som kvoten mellan två heltal. Roten ur 2 är vad man senare kom att kalla för ett irrationellt tal. Irrationellt för att det är bortom det begripliga, bortom förnuftet, bortom det rationella.
Exakt när och vem som insåg att roten ur 2 inte kan skrivas som ett rationellt tal är fortfarande oklart, men enligt legenden var upptäckten så chockerande att pythagoréerna lät mörda Hippasus som straff för att han bevisat att roten ur två var irrationellt, och för att förhindra att kunskapen spreds. Men om detta vet vi väldigt lite.
För moderna människor måste mordet på Hippasus betraktas som en överreaktion. Nog fanns det större problem att bekymras sig över också på den tiden.
Men samtidigt finns det något fascinerande i det faktum att roten ur 2 inte kunde skrivas som ett rationellt tal. Det innebär nämligen att talföljden som beskriver roten ur 2 är oändlig. 1,4142 ... ja, du ser på illustrationen här nedanför hur de de första 1 000 decimalerna ser ut.
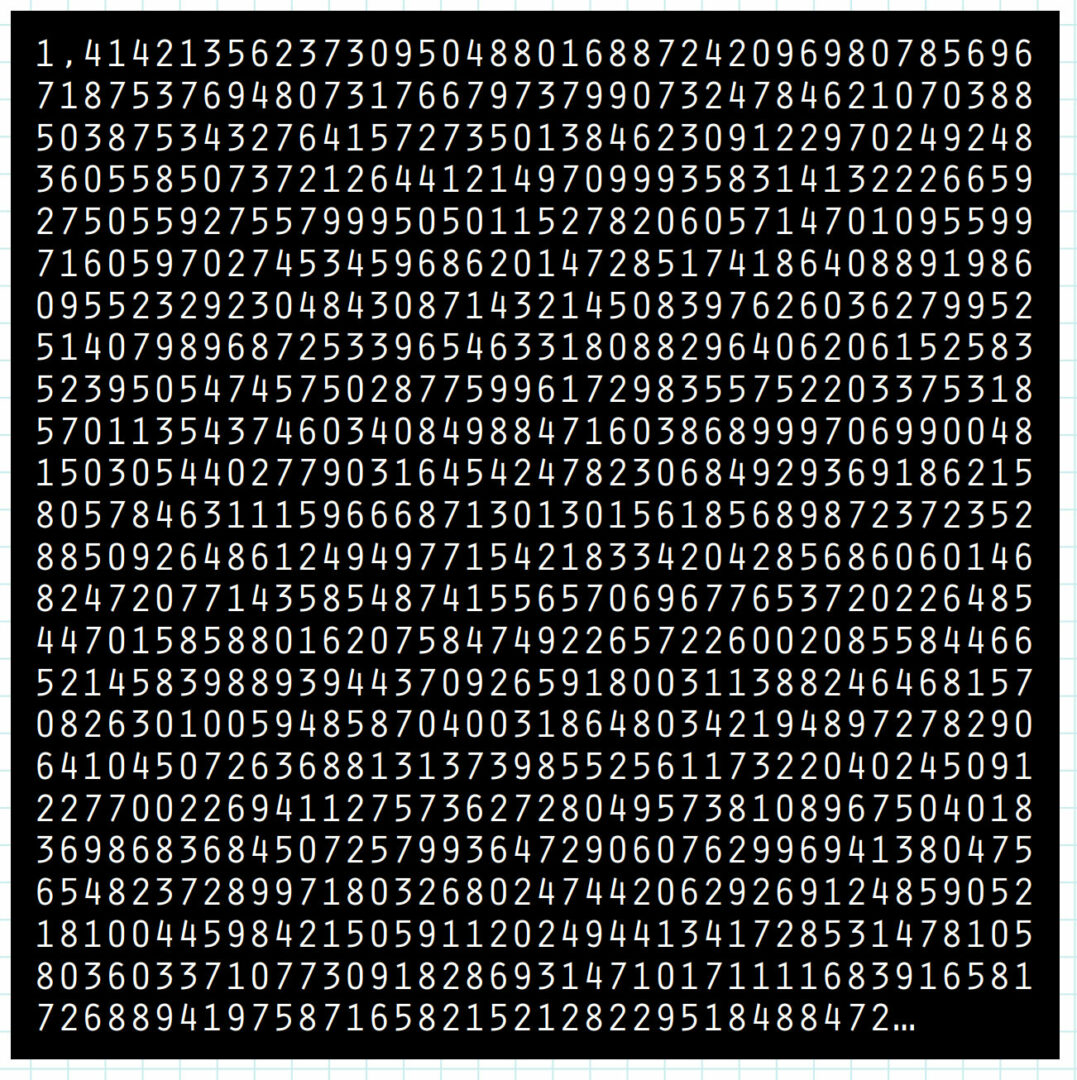
Är man nyfiken, eller känner sig riktigt nördig, kan man gå in på en hemsida från Nasa och titta på de första en miljon decimalerna … För några år sedan beräknades de första tio tusen miljarder decimalerna. Det låter mycket – tio tusen miljarder – men är ingenting i sammanhanget, långt mindre än en fluga som pustar i en tropisk orkan.
Talserien bara fortsätter utan att upprepa sig. De tal som följer på varandra är slumpmässigt ordnade (man tror sig också vara nästan helt säker på att alla tal som uppträder i decimalutvecklingen gör det med lika stor frekvens, alltså det ska finnas lika många, säg, treor som femmor i utvecklingen, men det har formellt sett inte bevisats än).
Men om talserien bara fortsätter kan man fråga vad det är för hemligheter den döljer. Vad är sannolikheten att min ytterst hemliga bankkontokod ska finnas där? Ja, en bankkontokod har fyra siffror och det finns då 10 000 möjliga kombinationer. Sannolikheten att den ska dyka upp direkt är således en på 10 000, alltså ganska osannolik. Men roten ur två är ett långt tal, och sannolikheten att min kombination dyker upp i talserien ökar ju längre vi letar. Och redan bland den första miljonen decimaler visar det sig att den dyker upp, drygt 100 gånger till och med.
Så här kan man resonera kring längre tal, säg vad är sannolikheten att 2001-09-11 finns i talserien? Så långa tal är ju betydligt mer osannolika, men eftersom roten ur 2 fortsätter in i evigheten blir sannolikheten att de ska hittas allt större ju längre man letar och närmar sig långsamt hundra procent. Det här innebär att alla telefonnummer, personnummer och bankkontonummer, jag, mina vänner och familj, någonsin haft – med allra största sannolikhet – kommer uppenbara sig i talserien som definierar roten ur 2.
Om vi dessutom ordnar ett tal till varje bokstav så att a=01, b=02, … till ö=28, och så vidare med versaler och skiljetecken kommer alla möjliga texter och skrifter, inklusive Shakespeares samlade verk, med allra största sannolikhet, någonstans långt där borta på väg mot evigheten, uppenbara sig i den talserie som definierar roten ur 2.
Man förstår nu kanske bättre varför pythagoréerna ryggade tillbaka när de insåg vad det var för märkligt tal de hade stött på.
Slumpen och oändlighetens samlade kraft är vidunderlig.
***
Teckna din prenumeration på Fokus här.
Det oändliga har alltid fascinerat mänskligheten. Är universum till exempel oändligt stort eller är det begränsat? Och om det är begränsat, vad finns då bortom denna gräns?
Liknande frågor har man ställt sig inom matematiken. Det började med de naturliga talen, alltså 0,1,2,3,4 etcetera. Den här serien fortsätter in i evigheten, eftersom vilket tal man än väljer som det största alltid kan adderas med ytterligare tal, och vips har vi ett större tal. Med andra ord, det finns oändligt många heltal.
Matematiska skönheter
Detta är första delen av tre i artikelserien om matematiska skönheter. Läs den andra delen här.
Oändligheten har ett antal märkliga egenskaper. Fundera över vad som händer om vi skulle stryka alla jämna tal från denna lista? Ja då har vi kvar alla ojämna. Men det finns oändligt många både jämna och ojämna tal. Det innebär att om vi tar bort oändligt många tal (alla de jämna), från alla heltal har vi fortfarande oändligt många kvar, med andra ord:
Oändligheten minus oändligheten = oändligheten.
Oändlighetens vindlingar hyser fler smaragder. Låt mig påminna om operationen roten ur.
Roten ur 9 är alltså 3, eftersom om vi multiplicerar 3 med sig självt så får vi tillbaka nio. Det här gäller för alla tal. Roten ur 16 är sålunda 4, och roten ur 100 är 10.
Men fundera nu över vad som händer om man tar roten ur 2. Vilket tal multiplicerat med sig självt blir 2?
Här får man pröva sig fram. Testar man 1,4 hamnar man nära, eftersom 1,4 x 1,4 = 1,96. Vidare har vi att 1,5 x 1,5 = 2,25, så det blir något för stort. Roten ur 2 måste alltså vara större än 1,4 men mindre än 1,5. Letar man länge och väl, eller testar med miniräknare eller smartphone, kommer man fram till ett svar på ungefär 1,414213…
Antikens matematiker har intresserat sig för det här talet länge. Det har att göra med att det uppträder i geometrin på ett högst konkret sätt. Har man en kvadrat med sidorna ett blir diagonalen exakt lika med roten ur 2. Talet är sålunda också av stort praktiskt värde när man ska beräkna avstånd.
Redan babylonierna lyckades för 3 700 år sedan komma fram till en mycket bra approximation. Deras uppskattning skiljer sig från det korrekta värdet med ungefär en miljondel. Det är en imponerande prestation. En lertavla med detta resultat, kallad YBC7289, finns bevarad vid Yale Babylonian Collection.
Lite drygt tusen år senare verkade pythagoréerna, en grupp tänkare som hade samlats kring Pythagoras, i det antika Grekland. De ägnade sig åt matematik, filosofi, musik och andra sköna konster och de påminde också om ett slags sekt där de naturliga talen (heltalen plus nollan) utgjorde en form av ramverk, en byggställning kring vilken hela världen gick att byggas upp och förstå.
Tal som exempelvis 0,5 och 0,25 gick att skriva som kvoten mellan två heltal och på så sätt kunde man bygga upp aritmetiken. I pythagoréernas världsbild var alla tal antingen heltal eller kvoter mellan dem. I dag kallar vi dessa tal för rationella, det syftar på de tal som kan skrivas som en kvot mellan två heltal.
Men snart insåg pythagoréerna att talet roten ur 2 inte passade in i denna bild. Det kunde nämligen inte beskrivas som kvoten mellan två heltal. Roten ur 2 är vad man senare kom att kalla för ett irrationellt tal. Irrationellt för att det är bortom det begripliga, bortom förnuftet, bortom det rationella.
Exakt när och vem som insåg att roten ur 2 inte kan skrivas som ett rationellt tal är fortfarande oklart, men enligt legenden var upptäckten så chockerande att pythagoréerna lät mörda Hippasus som straff för att han bevisat att roten ur två var irrationellt, och för att förhindra att kunskapen spreds. Men om detta vet vi väldigt lite.
För moderna människor måste mordet på Hippasus betraktas som en överreaktion. Nog fanns det större problem att bekymras sig över också på den tiden.
Men samtidigt finns det något fascinerande i det faktum att roten ur 2 inte kunde skrivas som ett rationellt tal. Det innebär nämligen att talföljden som beskriver roten ur 2 är oändlig. 1,4142 … ja, du ser på illustrationen här nedanför hur de de första 1 000 decimalerna ser ut.

Är man nyfiken, eller känner sig riktigt nördig, kan man gå in på en hemsida från Nasa och titta på de första en miljon decimalerna … För några år sedan beräknades de första tio tusen miljarder decimalerna. Det låter mycket – tio tusen miljarder – men är ingenting i sammanhanget, långt mindre än en fluga som pustar i en tropisk orkan.
Talserien bara fortsätter utan att upprepa sig. De tal som följer på varandra är slumpmässigt ordnade (man tror sig också vara nästan helt säker på att alla tal som uppträder i decimalutvecklingen gör det med lika stor frekvens, alltså det ska finnas lika många, säg, treor som femmor i utvecklingen, men det har formellt sett inte bevisats än).
Men om talserien bara fortsätter kan man fråga vad det är för hemligheter den döljer. Vad är sannolikheten att min ytterst hemliga bankkontokod ska finnas där? Ja, en bankkontokod har fyra siffror och det finns då 10 000 möjliga kombinationer. Sannolikheten att den ska dyka upp direkt är således en på 10 000, alltså ganska osannolik. Men roten ur två är ett långt tal, och sannolikheten att min kombination dyker upp i talserien ökar ju längre vi letar. Och redan bland den första miljonen decimaler visar det sig att den dyker upp, drygt 100 gånger till och med.
Så här kan man resonera kring längre tal, säg vad är sannolikheten att 2001-09-11 finns i talserien? Så långa tal är ju betydligt mer osannolika, men eftersom roten ur 2 fortsätter in i evigheten blir sannolikheten att de ska hittas allt större ju längre man letar och närmar sig långsamt hundra procent. Det här innebär att alla telefonnummer, personnummer och bankkontonummer, jag, mina vänner och familj, någonsin haft – med allra största sannolikhet – kommer uppenbara sig i talserien som definierar roten ur 2.
Om vi dessutom ordnar ett tal till varje bokstav så att a=01, b=02, … till ö=28, och så vidare med versaler och skiljetecken kommer alla möjliga texter och skrifter, inklusive Shakespeares samlade verk, med allra största sannolikhet, någonstans långt där borta på väg mot evigheten, uppenbara sig i den talserie som definierar roten ur 2.
Man förstår nu kanske bättre varför pythagoréerna ryggade tillbaka när de insåg vad det var för märkligt tal de hade stött på.
Slumpen och oändlighetens samlade kraft är vidunderlig.
***
Teckna din prenumeration på Fokus här.